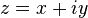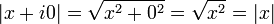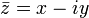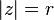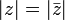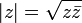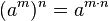La influencia e importancia de las matemáticas en la sociedad ha ido en constante crecimiento, en
buena parte debido al espectacular aumento de sus aplicaciones. Puede decirse que todo se matematiza.
No es concebible la innovación tecnológica, en el sentido actual de Investigación y Desarrollo, sin la
Asimismo, la enorme cantidad y variedad de la información que hoy debemos manejar plantea
nuevos problemas como la transmisión de dicha información, su protección, su comprensión, su
codificación, su clasificación, etc., los cuales sólo pueden tener un tratamiento efectivo a través de los
complejos algoritmos matemáticos que se han desarrollado bajo la exigencia de las nuevas necesidades
planteadas.
De este modo, los sistemas educativos de cada país deben concentrarse en las habilidades y en
aquellos procesos que les den a los jóvenes el acceso al conocimiento, para entender, criticar y
transformarlo. De ahí que la enseñanza de las matemáticas con la del español ocupen un lugar estratégico
en la formación diseñada por los currículos de diversos países, incluyendo una participación sustancial en la
carga horaria semanal.
TEMA 1.
A) PROPOSICIONES
B) CONECTORES LOGICOS
C) TABLA DE VERDAD
A) En el idioma científico, una proposiciòn se refiere a un enunciado que puede ser verdadero o falso, generalmente una oración enunciativa, base de lo que constituye el lenguaje formal de la lógica simbólica.
Una proposición lógica es Expresión enunciativa a la que puede atribuirse un sentido o función lógica de verdad o falsedad.
EXISTEN DOS TIPOS DE PROPOSICIONES:
- Proposiciones simples:
- Proposiciones compuestas:
Proposiciones Simples Y Compuestas
1.1. Proposiciones simples y proposiciones compuestas
En la lógica se distinguen dos tipos de proposiciones, siendo estas:
Proposiciones Simples o atómicas.
Proposiciones Compuestas o Moleculares.
Antes de iniciar el tratamiento de estos dos tipos de proposiciones, se dará la
definición de los que es una proposición:
Como ejemplos de proposiciones se dan los siguientes:
1. 4 es menor que ocho
2. Carlos es alto
3. México es un país de América
4. 6 es mayor que 10
5. María es inteligente
6. El sábado no hay clases
7. 5 más 11 es 16
8. El uno es el primer número natural
Ahora se dan algunas expresiones que no son proposiciones:
1. ¿Cómo te llamas?
2. ¿Qué hora es?
3. UPIICSA
4. El árbol
5. ¡Levanta esa pluma!
Lógica es el conjunto de los métodos y principios usados para
distinguir el razonamiento correcto del incorrecto.
Proposición es la oración afirmativa que puede ser verdadera o falsa,
pero no ambas. Estas expresiones no son proposiciones porque no afirman nada que sea
verdadero o falso, es decir, la 1 y 2 son preguntas, la 3 y 4 son frases y la 5 es
una orden.
Ejemplos de proposiciones simples o atómicas:
1. La ballena es roja
2. La raíz cuadrada de 16 es 4
3. Gustavo es alto
4. Teresa va a la escuela
Ejemplos de proposiciones compuestas:
1. La ballena no es roja
2. Gustavo no es alto
3. Teresa va a la escuela o María es inteligente
4. 4 es menor que 8 o 6 es mayor que 10
5. El 1 es el primer número primo y es mayor que cero
6. El 7 es mayor que 5 y 7 es menor que 10
7. Si Yolanda es estudiosa entonces pasará el examen
8. Si corro rápido entonces llegaré temprano
9. Terminaré rápido si y sólo si me doy prisa
10. Aprenderé Matemáticas si y sólo si estudio mucho
En la lógica se distinguen dos tipos de proposiciones, siendo estas:
Proposiciones Simples o atómicas.
Proposiciones Compuestas o Moleculares.
Antes de iniciar el tratamiento de estos dos tipos de proposiciones, se dará la
definición de los que es una proposición:
Como ejemplos de proposiciones se dan los siguientes:
1. 4 es menor que ocho
2. Carlos es alto
3. México es un país de América
4. 6 es mayor que 10
5. María es inteligente
6. El sábado no hay clases
7. 5 más 11 es 16
8. El uno es el primer número natural
Ahora se dan algunas expresiones que no son proposiciones:
1. ¿Cómo te llamas?
2. ¿Qué hora es?
3. UPIICSA
4. El árbol
5. ¡Levanta esa pluma!
Lógica es el conjunto de los métodos y principios usados para
distinguir el razonamiento correcto del incorrecto.
Proposición es la oración afirmativa que puede ser verdadera o falsa,
pero no ambas. Estas expresiones no son proposiciones porque no afirman nada que sea
verdadero o falso, es decir, la 1 y 2 son preguntas, la 3 y 4 son frases y la 5 es
una orden.
Ejemplos de proposiciones simples o atómicas:
1. La ballena es roja
2. La raíz cuadrada de 16 es 4
3. Gustavo es alto
4. Teresa va a la escuela
Ejemplos de proposiciones compuestas:
1. La ballena no es roja
2. Gustavo no es alto
3. Teresa va a la escuela o María es inteligente
4. 4 es menor que 8 o 6 es mayor que 10
5. El 1 es el primer número primo y es mayor que cero
6. El 7 es mayor que 5 y 7 es menor que 10
7. Si Yolanda es estudiosa entonces pasará el examen
8. Si corro rápido entonces llegaré temprano
9. Terminaré rápido si y sólo si me doy prisa
10. Aprenderé Matemáticas si y sólo si estudio mucho
B) Conectivos Lógicos (Términos de Enlace)
“Son palabras y/o símbolos que enlazan proposiciones con el fin de construir un lenguajes (verbal o simbólico) más amplio”. Los conectivos lógicos más usuales son:
Simbolo Palabra Nombre
(), [] agrupacion¬ No, no es, cierto Negacion
Conectivos lógicos y proposiciones compuestas.
Existen conectores u operadores lógicas que permiten formar proposiciones compuestas (formadas por varias proposiciones). Los operadores o conectores básicos son:
Operador and (y)
Se utiliza para conectar dos proposiciones que se deben cumplir para que se pueda obtener un resultado verdadero. Si símbolo es: {Ù , un punto (.), un paréntesis}. Se le conoce como la multiplicación lógica:
Ejemplo.
Sea el siguiente enunciado "El coche enciende cuando tiene gasolina en el tanque y tiene corriente la batería"
Sean:
p: El coche enciende.
q: Tiene gasolina el tanque.
r: Tiene corriente la batería.
De tal manera que la representación del enunciado anterior usando simbología lógica es como sigue:
p = q Ù r
Su tabla de verdad es como sigue:
q | r | p = q Ù r |
1 | 1 | 1 |
1 | 0 | 0 |
0 | 1 | 0 |
0 | 0 | 0 |
1 = verdadero
0 = falso
En la tabla anterior el valor de q=1 significa que el tanque tiene gasolina, r=1 significa que la batería tiene corriente y p = q Ù r=1 significa que el coche puede encender. Se puede notar que si q o r valen cero implica que el auto no tiene gasolina y que por lo tanto no puede encender.
q | r | p = q Ù r |
1 | 1 | 1 |
1 | 0 | 0 |
0 | 1 | 0 |
0 | 0 | 0 |
Con este operador se obtiene un resultado verdadero cuando alguna de las proposiciones es verdadera. Se eindica por medio de los siguientes símbolos: {Ú ,+,È }. Se conoce como las suma lógica. Ejemplo.
Sea el siguiente enunciado "Una persona puede entrar al cine si compra su boleto u obtiene un pase". Donde.
p: Entra al cine.
q: Compra su boleto.
r: Obtiene un pase.
q | r | p =q Ú r |
1 | 1 | 1 |
1 | 0 | 1 |
0 | 1 | 1 |
0 | 0 | 0 |
Su función es negar la proposición. Esto significa que sí alguna proposición es verdadera y se le aplica el operador not se obtendrá su complemento o negación (falso). Este operador se indica por medio de los siguientes símbolos: {‘, Ø ,- }. Ejemplo.
p | p’ |
1 | 0 |
0 | 1 |
En este momento ya se pueden representar con notación lógica enunciados más complejos. Ejemplo
Sean las proposiciones:
p: Hoy es domingo.
q: Tengo que estudiar teoría del aprendizaje.
r: Aprobaré el curso.
El enunciado: "Hoy es domingo y tengo que estudiar teorías de aprendizaje o no aprobaré el curso". Se puede representar simbólicamente de la siguiente manera:
p Ù qÚ r
Por otro lado con ayuda de estos operadores básicos se pueden formar los operadores compuestos Nand (combinación de los operadores Not y And), Nor (combina operadores Not y Or) y Xnor (resultado de Xor y Not).
c)
Tablas de verdad.
En estos momentos ya se está en condiciones de elaborar cualquier tabla de verdad. A continuación se presenta un ejemplo para la proposición [(p® q)Ú (q’Ù r) ] « (r® q).
p | q | r | q’ | p® q | (q’Ù r) | (p® q)Ú (q’Ù r) | r® q | [(p® q)Ú (q’Ù r) ] « (r® q) |
0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 |
0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 |
0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 |
1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 |
1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 |
1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 |
El número de líneas de la tabla de verdad depende del número de variables de la expresión y se puede calcular por medio de la siguiente formula.
No de líneas = 2n Donde n = número de variables distintas.
Es importante destacar a medida que se avanza en el contenido del material el alumno deberá participar activamente. Estos significa que cuando se esta definiendo proposiciones y características propias de ellas, además de los ejemplos que el maestro explique, el alumno deberá citar proposiciones diferentes, deberá entender el porque un enunciado no es válido. Cuando se ven conectores lógicos, los alumnos deberán saber emplearlos en la representación de proposiciones más complejas. Pero algo muy importante, es que los ejemplo que el maestro y los alumnos encuentren en la clase, deben ser de interés para el estudiante. Cuando se ven tablas de verdad el alumno deberá saber perfectamente bien el porque de cada uno de los resultados. En pocas palabras el conocimiento deberá ser significativo.Tautología y contradicción.
Tautología, es aquella proposición (compuesta) que es cierta para todos los valores de verdad de sus variables. Un ejemplo típico es la contrapositiva cuya tabla de verdad se indica a continuación.
p | q | p’ | q’ | p® q | q’® p’ | (p® q)« (q’® p’) |
0 | 0 | 1 | 1 | 1 | 1 | 1 |
0 | 1 | 1 | 0 | 1 | 1 | 1 |
1 | 0 | 0 | 1 | 0 | 0 | 1 |
1 | 1 | 0 | 0 | 1 | 1 | 1 |
Note que en las tautologías para todos los valores de verdad el resultado de la proposición es siempre 1. Las tautologías son muy importantes en lógica matemática ya que se consideran leyes en las cuales nos podemos apoyar para realizar demostraciones.
TEMA 2.
A) SISTEMAS NUMÉRICOS
A) SISTEMAS NUMÉRICOS
B) OPERACIONES BÁSICAS
C) NÚMEROS REALES
Los sistemas de numeración son conjuntos de dígitos usados para representar cantidades, así se tienen los sistemas de numeración decimal, binario, octal, hexadecimal, romano, etc. Los cuatro primeros se caracterizan por tener una base (número de dígitos diferentes: diez, dos, ocho, dieciseis respectivamente) mientras que el sistema romano no posee base y resulta más complicado su manejo tanto con números, así como en las operaciones básicas.
Los sistemas de numeración que poseen una base tienen la característica de cumplir con la notación posicional, es decir, la posición de cada número le da un valor o peso, así el primer dígito de derecha a izquierda después del punto decimal, tiene un valor igual a b veces el valor del dígito, y así el dígito tiene en la posición n un valor igual a: (bn) * A
donde:
b = valor de la base del sistema
n = número del dígito o posición del mismo
A = dígito.
Por ejemplo:
digitos: 1 2 4 9 5 3 . 3 2 4
posicion 5 4 3 2 1 0 . -1 -2 -3
C) NÚMEROS REALES
A)
Sistemas NuméricosLos sistemas de numeración que poseen una base tienen la característica de cumplir con la notación posicional, es decir, la posición de cada número le da un valor o peso, así el primer dígito de derecha a izquierda después del punto decimal, tiene un valor igual a b veces el valor del dígito, y así el dígito tiene en la posición n un valor igual a: (bn) * A
donde:
b = valor de la base del sistema
n = número del dígito o posición del mismo
A = dígito.
Por ejemplo:
digitos: 1 2 4 9 5 3 . 3 2 4
posicion 5 4 3 2 1 0 . -1 -2 -3
B) En primer lugar analicemos como se realiza la operación suma en base decimal para que este criterio nos sirva como modelo de referencia.
11
7842
+ 7437
----
15279
Como se observa para sumar dos numeros si la suma excede al valor de la base existe un acarreo o arrastre de una unidad en la columna izquierda siguiente. En cualquier otra base se hara de forma analoga, esto es, se suma de derecha a izquierda los numeros de cada una de las columnas, incluyendo el posible arrastre, como si se tratase de la base decimal y seguidamente el resultado obtenido N se convierte a la base deseada.SUMA EN EL SISTEMA OCTAL.11 ***NOTA*** los numeros que superen a 1742 el numero de la base se dividen entre +5063 la base que en este caso es base 8, y ---- y el cociente se suma a la sig 7025 columna y el reciduo es el resultado2+3=5, 4+6=10 10/8, 1+7+0=8 8/8, 1+1+5=7
C) Los números naturales surgen de la necesidad de contar, de enumerar: |
- Con los números naturales
se puede sumar. De hecho, con la operación suma, los naturales forman un SEMIGRUPO CONNOTATIVO.
- Con la operación producto los naturales también tienen estructura de semigrupo conmutativo.
- El infinito de los números naturales se denomina infinito numerable. Cualquier conjunto que pueda ponerse en correspondencia biyectiva con el conjunto de los números naturales se dice que es infinito numerable. Por ejemplo, el conjunto de las potencias sucesivas de un número
, es decir, el conjunto
cuando
es distinto de 0, 1 y -1, es un conjunto infinito numerable. El conjunto de los números enteros y el de los racionales también son infinitos numerables como se verá más adelante.
- El conjunto de los naturales es un conjunto totalmente ordenado, es decir, existe una RELACIÓN DE ORDEN TOTAL, lo que significa que existe una relación de orden y que dos elementos cualesquiera pueden ser siempre comparados entre sí usando dicha relación. Dicho de otra forma, dados dos naturales,
e
, o bien
, o bien
.
no vacío del conjunto de los naturales tiene un elemento mínimo, esto es, existe un elemento
tal que para todo
de
se tiene
.
Por ejemplo, el subconjunto formado por los números pares tiene como elemento mínimo a 2.
TEMA 3.
A) NÚMEROS ENTEROS
B) FRACCIONARIOS
| Cuando se necesita además restar surgen los números enteros |
- Los enteros se obtienen a partir de los naturales añadiendo los opuestos para la operación suma.
el entero positivo a-b, si a > b,0, si a=bel entero negativo -(b-a) si a < bLa suma de dos enteros negativos se define como (-a)+(-b)=-(a+b)De hecho, los enteros, con la operación suma tienen estructura de GRUPO CONMUTATIVO.
- (-a)(-b)=ab
- (-a)b=a(-b)=-(ab),
el conjunto de los enteros, con ambas operaciones tiene estructura de ANILLO CONMUTATIVO Y CON UNIDAD., por ejemplo como ésta:
si n es un entero positivo
Por tanto, el conjunto de los enteros es también infinito numerable. También es un conjunto totalmente ordenado, cuando se considera la relación de orden definida en la forma obvia y que extiende la relación de orden que se tiene en. También es cierto que en los enteros todo subconjunto acotado interiormente tiene elemento mínimo, y recíprocamente, todo subconjunto acotado superiormente tiene elemento máximo.
B) ¿Que son los Numeros Fraccionarios?
Los Numeros Fraccionarios , son el cociente indicado
a/b
de dos números enteros que se llaman numerador, a, y denominador, b. Ha de ser b ≠ 0.
Por ejemplo, en la fracción 3/5 el denominador, 5, indica que son “quintas partes”, es decir, denomina el tipo de parte de la unidad de que se trata; el numerador, 3, indica cuántas de estas partes hay que tomar: “tres quintas partes”.
Si el numerador es múltiplo del denominador, la fracción representa a un número entero:
14/2=7; -15/3=-5; 352/11= 32
Dos fracciones a/b y a'/b' son equivalentes, y se expresa
a/b = a'/b'
si a · b′ = b · a′.
Así,
21/28= 9/12
porque 21 · 12 = 9 · 28 = 252.
Si el numerador y el denominador de una fracción son divisibles por un mismo número, d, distinto de 1 o -1, al dividirlos por d se obtiene otra fracción equivalente a ella. Se dice que la fracción se ha simplificado o se ha reducido:
a/b=a.d'/b.d'=a'/b'
Por ejemplo:
120/90= 12/9
La fracción 12/9 es el resultado de simplificar 120/90 dividiendo sus términos por 10
Se dice que una fracción es irreducible si su numerador y su denominador son números primos entre sí.
La fracción 3/5 es irreducible. La fracción 12/9 no es irreducible porque se puede simplificar:
12/= 4/3
Reducir dos o más fracciones a común denominador es obtener otras fracciones respectivamente equivalentes a ellas y que todas tengan el mismo denominador. Si las fracciones de las que se parte son irreducibles, el denominador común ha de ser un múltiplo común de sus denominadores. Si es el mínimo común múltiplo (m.c.m.) de ellos, entonces se dice que se ha reducido a mínimo común denominador.
Por ejemplo, para reducira común denominador las fracciones
2/3, 4/9 y 3/5
se puede tomar 90 como denominador común, con lo que se obtiene:
2/3=60/90, 4/9=40/90, 3/5=54/90
Es decir,
es el resultado de reducir las tres fracciones anteriores a un común denominador: 90.
Pero si en vez de 90 se toma como denominador común 45, que es el m.c.m. de 3, 9 y 5, entonces se obtiene
30/45, 20/45, 27/445
que es el resultado de reducir las tres fracciones a su mínimo común denominador.
Para sumar dos o más fracciones se reducen a común denominador, se suman los numeradores de éstas y se mantiene su denominador. Por ejemplo:
2/3+ 4/9 y+3/5 = 30/45+ 20/45+27/45 =30+20+27/45=77/45
El producto de dos fracciones es otra fracción cuyo numerador es el producto de sus numeradores y cuyo denominador es el producto de sus denominadores:
a/b * c/d = a*c/b*d
La inversa de una fracción a/b es otra fracción,b/a , que se obtiene permutando el numerador y el denominador. El producto de una fracción por su inversa es igual a 1:
a/b * b/a=a*b/b*a=1/1=1
Cociente de Fracción
El cociente de dos fracciones es el producto de la primera por la inversa de la segunda:
a/b : p/q , a/b*q/p, a*q/b*p
TEMA 4.
* OPERACIONES DE FRACCIONES (+, -, X, ÷)
Ejemplos
Producto de fracciones
1º Se multiplican los numeradores, este producto es el nuevo numerador.2º Se multiplican los denominadores, su producto es el nuevo denominador.3º Después se simplifica.Fracción de un número: Es una multiplicación de fracciones, el número tiene como denominador uno.Fracción de una fracción: Se multiplican las dos fracciones.Fracción inversa: Se le da la vuelta, el numerador pasa a ser el denominador y el numerador es el nuevo denominador. Una fracción multiplicada por su inversa da la unidad.División de fracciones
1º Multiplicamos el numerador de la primera por el denominador de la segunda, el producto es el nuevo numerador.2º Multiplicamos el denominador de la primera por el numerador de la segunda, el producto es el nuevo denominador.3º Después si podemos se simplifica.Ejemplos de multiplicación y división de fracciones
TEMA 5.
A) VALOR ABSOLUTO B) PROPIEDADES
A) Valor absoluto
Más ejemplos:
B)
Valor absoluto quiere decir...
... simplemente qué distancia hay de un número a cero:
 |
"6" está a 6 de cero, y "-6" también está a 6 de cero. Así que el valor absoluto de 6 es 6, y el valor absoluto de -6 también es 6 |
- El valor absoluto de -9 es 9
- El valor absoluto de 3 es 3
- El valor absoluto de -156 es 156
¡No negativos!
Así que en la práctica el "valor absoluto" significa quitar el signo negativo de delante de un número, y pensar en todos los números como números positivos.Símbolo de valor absoluto
Para indicar el valor absoluto de algo, pones símbolos "|" a los lados, como en estos ejemplos:| |-5| = 5 | |7| = 7 |
Restar de las dos maneras
No importa en qué orden hagas una resta, su valor absoluto siempre será el mismo:| |8-3| = 5 | |3-8| = 5 |
| (8-3 = 5) | (3-8 = -5, y |-5| = 5) |
B)
Propiedades fundamentales
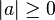
No negatividad 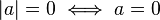
Definición positiva 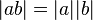
Propiedad multiplicativa 
Desigualdad triangular
Otras propiedades

Simetría 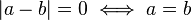
Identidad de discernibles 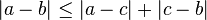
Desigualdad triangular 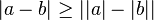
(equivalente a la propiedad aditiva) 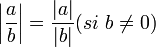
Preservación de la división (equivalente a la propiedad multiplicativa)
Valor absoluto de un número complejo
Como los números complejos no conforman un conjunto ordenado en el sentido de los reales, la generalización del concepto no es directa, sino que requiere de la siguiente identidad, que proporciona una definición alternativa y equivalente para el valor absoluto:
Propiedades
El valor absoluto de los complejos comparte todas las propiedades vistas anteriormente para los números reales. Además, si
Como los números reales positivos forman un subgrupo de los números complejos bajo el operador de multiplicación, podemos pensar en el valor absoluto como un endomorfismo del grupo multiplicativo de los números complejos.
TEMA 6.
* TRUCOS MATEMÁTICA
TEMA 7.
* POTENCIACION Y PROPIEDADES
Multiplicación de potencias de igual base
El producto de dos o más potencias de igual a base «a» es igual a la potencia de base a y exponente igual a la suma de los exponentes respectivos.
ejemplos:
División de Potencias de Igual Base
La división de dos potencias de igual base a es igual a la potencia de base a y exponente igual a la resta de los exponentes respectivos (la misma base y se restan los exponentes.
Potencia de una potencia
La potencia de una potencia de base a es igual a la potencia de base a elevada a la multiplicación de ambos exponentes -
Potencia de base 10
En las potencias con base 10, el resultado será la unidad seguida de tantos ceros como indica la cifra del exponente.
Ejemplos:
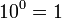
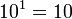

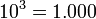
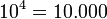


-
Potencia de un producto
La potencia de un producto es igual a cada uno de los factores del producto elevados al exponente de dicha potencia. Es decir, una potencia de base (a.b) y de exponente "n", es igual al factor "a" elevado a "n" por el factor "b" elevado a "n"
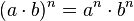

Propiedad distributiva
La potenciación es distributiva con respecto a la multiplicación y a la división:
pero no lo es con respecto a la suma ni a la resta.
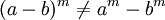
TEMA 8.* RADICACION Y PROPIEDADES
Si entendimos el concepto, ya es un gran paso, pero como es natural es apenas el principio.Tenemos algunas propiedades de radicación que conocer ahora, que nos permitirá avanzar y resolver mas eficientemente las distintas operaciones que se nos presente.* Simplificación o ampliación de índice de una raíz. Se puede dividir o multiplicar el índice de la raíz y el exponente de su base por un mismo número distinto de cero y el resultado no se modifica.* Propiedad cancelativa de los índicesSi dos raíces de igual índice son iguales, entonces sus bases son iguales* Raíz de raízLa raíz de una raíz es otra raíz de la misma base cuyo índice es el producto de los índices dados.ejemplo.Si tengo expresado, raiz cuadrada de raiz tercera de 64, lo que hago es multimplicar los índices, o sea 2 x 3 lo cual me quedará, raíz sexta de de 64. Resultado = 2* Propiedad distributivaLa radicación es distributiva respecto de la multimplicación y la división.Es decir que si tengo raiz cuadrada de 3 x 4, es lo mismo que expresar, raiz cuadrada de 3 por raíz cuadrada de 4.TEMA 9.A) EXPRESIONES ALGEBRAICASB) OPERACIONES SUMA, RESTA, MULTIPLICACIÓN, DIVICION.A) Trabajar en álgebra consiste en manejar relaciones numéricas en las que una o más cantidades son desconocidas. Estas cantidades se llaman variables, incógnitas o indeterminadas y se representan por letras.Una expresión algebraica es una combinación de letras y números ligadas por los signos de las operaciones: adición, sustracción, multiplicación, división y potenciación.Las expresiones algebraicas nos permiten, por ejemplo, hallar áreas y volúmenes.Longitud de la circunferencia: L = 2
Se puede dividir o multiplicar el índice de la raíz y el exponente de su base por un mismo número distinto de cero y el resultado no se modifica.* Propiedad cancelativa de los índicesSi dos raíces de igual índice son iguales, entonces sus bases son iguales* Raíz de raízLa raíz de una raíz es otra raíz de la misma base cuyo índice es el producto de los índices dados.ejemplo.Si tengo expresado, raiz cuadrada de raiz tercera de 64, lo que hago es multimplicar los índices, o sea 2 x 3 lo cual me quedará, raíz sexta de de 64. Resultado = 2* Propiedad distributivaLa radicación es distributiva respecto de la multimplicación y la división.Es decir que si tengo raiz cuadrada de 3 x 4, es lo mismo que expresar, raiz cuadrada de 3 por raíz cuadrada de 4.TEMA 9.A) EXPRESIONES ALGEBRAICASB) OPERACIONES SUMA, RESTA, MULTIPLICACIÓN, DIVICION.A) Trabajar en álgebra consiste en manejar relaciones numéricas en las que una o más cantidades son desconocidas. Estas cantidades se llaman variables, incógnitas o indeterminadas y se representan por letras.Una expresión algebraica es una combinación de letras y números ligadas por los signos de las operaciones: adición, sustracción, multiplicación, división y potenciación.Las expresiones algebraicas nos permiten, por ejemplo, hallar áreas y volúmenes.Longitud de la circunferencia: L = 2 r, donde r es el radio de la circunferencia.Área del cuadrado: S = l2, donde l es el lado del cuadrado.Volumen del cubo: V = a3, donde a es la arista del cubo.
r, donde r es el radio de la circunferencia.Área del cuadrado: S = l2, donde l es el lado del cuadrado.Volumen del cubo: V = a3, donde a es la arista del cubo.Expresiones algebraicas comunes
El doble o duplo de un número: 2xEl triple de un número: 3xEl cuádruplo de un número: 4xUn tercio de un número: x/3.Un cuarto de un número: x/4.Un número es proporcional a 2, 3, 4, ...: 2x, 3x, 4x,..Un número al cuadrado: x2Un número al cubo: x3Dos números consecutivos: x y x + 1.Dos números consecutivos pares: 2x y 2x + 2.Dos números consecutivos impares: 2x + 1 y 2x + 3.Descomponer 24 en dos partes: x y 24 − x.La suma de dos números es 24: x y 24 − x.La diferencia de dos números es 24: x y 24 + x.El producto de dos números es 24: x y 24/x.El cociente de dos números es 24; x y 24 · x.Valor numérico de una expresión algebraica
El valor númerico de una expresión algebraica, para un determinado valor, es el número que se obtiene al sustituir en ésta por valor numérico dado y realizar las operaciones indicadas.L(r) = 2 rr = 5 cm. L (5)= 2 ·
rr = 5 cm. L (5)= 2 · · 5 = 10
· 5 = 10 cmS(l) = l2l = 5 cm A(5) = 52 = 25 cm2a = 5 cm V(5) = 53 = 125 cm3
cmS(l) = l2l = 5 cm A(5) = 52 = 25 cm2a = 5 cm V(5) = 53 = 125 cm3Tipos de expresiones algebraicas
Monomio
Un monomio es una expresión algebraica formada por un solo término.Binomio
Un binomio es una expresión algebraica formada por dos términos.Trinomio
Un trinomio es una expresión algebraica formada por tres términos.Polinomio
Un polinomio es una expresión algebraica formada por más de un término.B) Suma o resta de monomios: Para sumar o restar monomios es necesario que sean semejantes. Monomios semejantes son aquellos que tienen la misma parte literal y el mismo grado. Ej: 2×3 + 5×3 - 6×3.Para hacer la operación sumamos los coeficientes y dejamos la misma parte literal. Ej: 2×3 + 5×3 - 6×3 = x3.Multiplicación de monomios: Para multiplicar monomios no es necesario que sean semejantes. Para ello se multiplican los coeficientes, se deja la misma parte literal y se suman los grados. Ej: 3xy.4×2y3= 12×3y4 División de monomios: Para dividir dos monomios, se dividen los coeficientes, se deja la misma parte literal y se restan los grados. Ej: 4×5y3:2×2y= 2×3y2Suma de polinomios: Para sumar polinomios colocaremos cada monomio debajo de los que son semejantes y sumaremos sus coeficientes.Ej: 7×5+0×4+3×3+4×2–2x5×5+0×4+0×3 -x2 -x12×5+0×4+3×3+3×2–3xMultiplicación de polinomios: Para multiplicar polinomios haremos lo mismo que para multiplicar monomios, multiplicamos los coeficientes y sumamos los grados de las letras que son iguales.Si son varios los polinomios que tenemos que multiplicar haremos lo mismo pero pondremos los que son semejantes debajo unos de otros y los sumaremos al final.Ej: P(x)= 2×5+3×4–2×3-x2+2xQ(x)= 2×3P(x).Q(x)= 4×8+6×7–4×6–2×5+4×4TEMA 10.*) PRODUCTOS NOTABLES
División de monomios: Para dividir dos monomios, se dividen los coeficientes, se deja la misma parte literal y se restan los grados. Ej: 4×5y3:2×2y= 2×3y2Suma de polinomios: Para sumar polinomios colocaremos cada monomio debajo de los que son semejantes y sumaremos sus coeficientes.Ej: 7×5+0×4+3×3+4×2–2x5×5+0×4+0×3 -x2 -x12×5+0×4+3×3+3×2–3xMultiplicación de polinomios: Para multiplicar polinomios haremos lo mismo que para multiplicar monomios, multiplicamos los coeficientes y sumamos los grados de las letras que son iguales.Si son varios los polinomios que tenemos que multiplicar haremos lo mismo pero pondremos los que son semejantes debajo unos de otros y los sumaremos al final.Ej: P(x)= 2×5+3×4–2×3-x2+2xQ(x)= 2×3P(x).Q(x)= 4×8+6×7–4×6–2×5+4×4TEMA 10.*) PRODUCTOS NOTABLES
Sabemos que se llama producto al resultado de una multiplicación. También sabemos que los valores que se multiplican se llaman factores. Se llama productos notables a ciertas expresiones algebraicas que se encuentran frecuentemente y que es preciso saber factorizarles a simple vista; es decir, sin necesidad de hacerlo paso por paso. Se les llama productos notables (también productos especiales) precisamente porque son muy utilizados en los ejercicios. A continuación veremos algunas expresiones algebraicas y del lado derecho de la igualdad se muestra la forma de factorizarlas (mostrada como un producto notable). Cuadrado de la suma de dos cantidades o binomio cuadradoProductos notables
El cuadrado de la suma de dos cantidades es igual al cuadrado de la primera cantidad, más el doble de la primera cantidad multiplicada por la segunda, más el cuadrado de la segunda cantidad. Demostración:a2 + 2ab + b2 = (a + b)2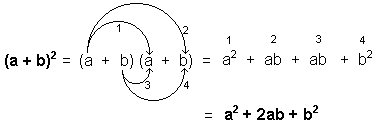 Entonces, para entender de lo que hablamos, cuando nos encontramos con una expresión de la forma a2 + 2ab + b2 debemos identificarla de inmediato y saber que podemos factorizarla como (a + b)2 Nota: Se recomienda volver al tema factorizarla para reforzar su comprensión. Cuadrado de la diferencia de dos cantidades
Entonces, para entender de lo que hablamos, cuando nos encontramos con una expresión de la forma a2 + 2ab + b2 debemos identificarla de inmediato y saber que podemos factorizarla como (a + b)2 Nota: Se recomienda volver al tema factorizarla para reforzar su comprensión. Cuadrado de la diferencia de dos cantidades
El cuadrado de la diferencia de dos cantidades es igual al cuadrado de la primera cantidad, menos el doble de la primera cantidad multiplicada por la segunda, más el cuadrado de la segunda cantidad. Demostración: Entonces, para entender de lo que hablamos, cuando nos encontramos con una expresión de la forma a2 – 2ab + b2 debemos identificarla de inmediato y saber que podemos factorizarla como (a – b)2 Producto de la suma por la diferencia de dos cantidades (o producto de dos binomios conjugados)a2 – 2ab + b2 = (a – b)2
El producto de la suma por la diferencia de dos cantidades es igual al cuadrado de la primera cantidad, menos el cuadrado de la segunda Demostración:(a + b) (a – b) = a2 – b2Entonces, para entender de lo que hablamos, cuando nos encontramos con una expresión de la forma (a + b) (a – b) debemos identificarla de inmediato y saber que podemos factorizarla como a2 – b2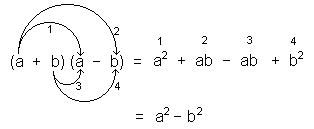
Otros casos de productos notable (o especiales):
Producto de dos binomios con un término común, de la forma
Demostración:x2 + (a + b)x + ab = (x + a) (x + b)Veamos un ejemplo explicativo: Tenemos la expresión algebraica x2 + 9 x + 14 obtenida del producto entre (x + 2) (x + 7 ) ¿Cómo llegamos a la expresión? a) El cuadrado del término común es (x)(x) = x2 b) La suma de términos no comunes multiplicada por el término común es (2 + 7)x = 9x c) El producto de los términos no comunes es (2)(7) = 14 Así, tenemos: x2 + 9 x + 14 = (x + 2) (x + 7 ) Entonces, para entender de lo que hablamos, cuando nos encontramos con una expresión de la forma x2 + (a + b)x + ab debemos identificarla de inmediato y saber que podemos factorizarla como (x + a) (x + b)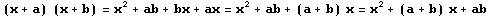 Producto de dos binomios con un término común, de la forma
Producto de dos binomios con un término común, de la forma
Demostración:x2 + (a – b)x – ab = (x + a) (x – b)Entonces, para entender de lo que hablamos, cuando nos encontramos con una expresión de la forma x2 + (a – b)x – ab debemos identificarla de inmediato y saber que podemos factorizarla como (x + a) (x – b). Producto de dos binomios con un término común, de la forma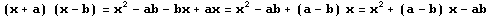
Demostración:x2 – (a + b)x + ab = (x – a) (x – b)Entonces, para entender de lo que hablamos, cuando nos encontramos con una expresión de la forma x2 – (a + b)x + ab debemos identificarla de inmediato y saber que podemos factorizar como (x – a) (x – b). Producto de dos binomios con un término común, de la forma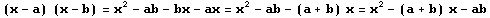
En este caso, vemos que el término común (x) tiene distinto coeficiente en cada binomio (mx y nx). Demostración:mnx2 + ab + (mb + na)x = (mx + a) (nx + b)Entonces, para entender de lo que hablamos, cuando nos encontramos con una expresión de la forma mnx2 + ab + (mb + na)x debemos identificarla de inmediato y saber que podemos factorizarla como (mx + a) (nx + b). Cubo de una suma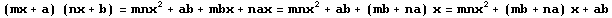
Entonces, para entender de lo que hablamos, cuando nos encontramos con una expresión de la forma a3 + 3a2b + 3ab2 + b3 debemos identificarla de inmediato y saber que podemos factorizarla como (a + b)3. Cubo de una diferenciaa3 + 3a2b + 3ab2 + b3 = (a + b)3a3 – 3a2b + 3ab2 – b3 = (a – b)3TEMA 11.- *) BELLEZA Y LAS MATEMÁTICAS
TEMA 12.
*) FACTORIZACION
Factorización |
Para entender la operación algebraica llamada factorización es preciso repasar los siguientes conceptos:
Cualquier expresión que incluya la relación de igualdad (=) se llama ecuación.
Una ecuación se denomina identidad si la igualdad se cumple para cualquier valor de las variables; si la ecuación se cumple para ciertos valores de las variables pero no para otros, la ecuación es condicional.
Un término es una expresión algebraica que sólo contiene productos de constantes y variables; 2x, – a, 3x son algunos ejemplos de términos.
La parte numérica de un término se denomina coeficiente.
Los coeficientes de cada uno de los ejemplos anteriores son 2, – 1, y 3.
Una expresión que contiene un solo término se denomina monomio; si contiene dos términos se llama binomio y si contiene tres términos, es un trinomio.
Un polinomio es una suma (o diferencia) finita de términos.
En este contexto, el grado es el mayor exponente de las variables en un polinomio. Por ejemplo, si el mayor exponente de la variable es 3, como en ax3 + bx2 + cx, el polinomio es de tercer grado.
Una ecuación lineal en una variable es una ecuación polinómica de primer grado; es decir, una ecuación de la forma ax + b = 0.
Se les llama ecuaciones lineales porque representan la fórmula de una línea recta en la geometria analitica.
Una ecuación cuadrática en una variable es una ecuación polinómica de segundo grado, es decir, de la forma ax2 + bx + c = 0.
Un número primo es un entero (número natural) que sólo se puede dividir exactamente por sí mismo y por 1. Así, 2, 3, 5, 7, 11 y 13 son todos números primos.
Las potencias de un número se obtienen mediante sucesivas multiplicaciones del número por sí mismo. El término a elevado a la tercera potencia, por ejemplo, se puede expresar como a·a·a o a3
Los factores primos de un cierto número son aquellos factores en los que éste se puede descomponer de manera que el número se puede expresar sólo como el producto de números primos y sus potencias.
Descomposición de números naturales en sus factores primos
Por ejemplo, un número natural como 20 puede expresarse como un producto de números de diferentes formas:
20 = 2 • 10 = 1 • 20 = 4 • 5
En cada uno de estos casos, los números que forman el producto son los factores.
Es decir, cuando expresamos el número 20 como el producto 2 • 10, a cada uno de los números (2 y 10) se les denomina factor.
En el caso de 1 • 20 los factores son 1 y 20 y finalmente en el caso de 4 • 5, los factores son 4 y 5.
Cada uno de los números 1, 2, 4, 5, 10, 20 se denominan a su vez divisores de 20.
Otro ejemplo, los factores primos de 15 son 3 y 5. Del mismo modo, como 60 = 22 • 3 • 5, los factores primos de 60 son 2, 3 y 5.
Debe recordarse, además, que cuando un número es divisible únicamente por sí mismo y por la unidad el número se denominaprimo.
Factorización y productos notables
Así como los números naturales pueden ser expresados como producto de dos o más números, los polinomios pueden ser expresadas como el producto de dos o más factores algebraicos.
 Cuando un polinomio no se puede factorizar se denomina irreducible. En los casos en que la expresión es irreducible, solo puede expresarse como el producto del número 1 por la expresión original.
Cuando un polinomio no se puede factorizar se denomina irreducible. En los casos en que la expresión es irreducible, solo puede expresarse como el producto del número 1 por la expresión original.Al proceso de expresar un polinomio como un producto de factores se le denomina factorización.
El proceso de factorización puede considerarse como inverso al proceso de multiplicar.
Factorizar, entonces, quiere decir identificar los factores comunes a todos los términos y agruparlos.
Los factores comunes son aquellos números que aparecen multiplicando a todos los términos de una expresión algebraica.
Estos números pueden estar dados explícitamente o representados por letras.
Así, factorizar un polinomio es descomponerlo en dos o más polinomios llamados factores, de tal modo que al multiplicarlos entre sí se obtenga el polinomio original.
En otras palabras, dada una expresión algebraica complicada, resulta útil, por lo general, el descomponerla en un producto de varios términos más sencillos.
Por ejemplo, 2x3 + 8x2y se puede factorizar, o reescribir, como 2x2(x + 4y).
Algunos ejemplos:
De la expresión ab2 + 3cb - b3 podemos factorizar b
y obtenemos la expresión: b(ab + 3c - b2) (1)
Veamos paso a paso cómo se obtuvo la expresión:
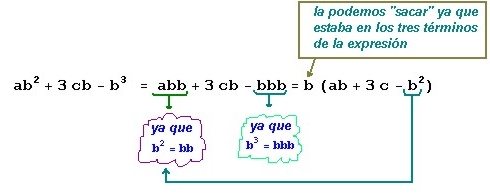
ahora podríamos reacomodar la expresión que queda dentro del paréntesis:
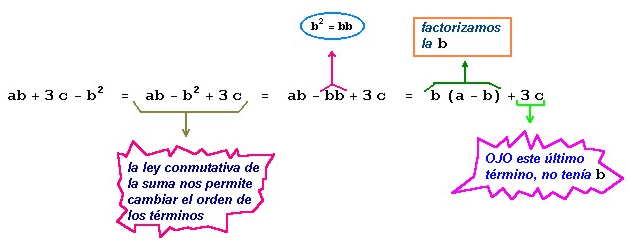
Finalmente si sustituimos este último resultado en (1), obtenemos:
ab2 + 3cb - b3 = b (b (a - b) + 3c)
ab2 + 3cb - b3 = b (ab - b2 + 3c)
ab2 + 3cb - b3 = b (ab +3c –b2)
Por otro lado, algunos productos sencillos que tienen una estructura determinada y que pueden ser evaluados de forma directa se denominan Productos notables.
En general los casos de factorización corresponden a los casos de productos notables.
 Antes de mostrar ejercicios de aplicación de factorización y productos notables, es necesario recordar la forma de hallar el máximo común divisor (mcd) de un conjunto de números dados.
Antes de mostrar ejercicios de aplicación de factorización y productos notables, es necesario recordar la forma de hallar el máximo común divisor (mcd) de un conjunto de números dados.Ejemplo: Determinar el máximo común divisor (mcd) de los números 56, 42 y 28.
El máximo común divisor de un conjunto de números dados corresponde al mayor número natural que los divide simultáneamente, con residuo cero.
Para hallar el mcd de un conjunto determinado de números, estos se dividen simultáneamente por los diferentes números primos (tomados en orden ascendente, y desechando los números primos por los cuales no se pueda hacer la división con residuo cero de todos los números de la fila) según el arreglo mostrado a continuación.
El proceso termina, cuando los números que aparecen en la fila inmediatamente inferior a la última división simultánea, no pueden dividirse simultáneamente por algún número primo.
El mcd buscado es el producto de los números primos que aparecen a la derecha:
56 | 42 | 28 | ÷ | 2 |
28 | 21 | 14 | ÷ | 7 |
4 | 3 | 2 | ||
Los números originales (56, 42, 28) se escriben desde la izquierda hacia la derecha.
A la derecha de ellos se escribe el 2 (primer número primo de la lista) y se divide cada uno de estos números por 2, escribiendo el resultado obtenido en la misma columna del número original.
La segunda fila muestra estos resultados.
Como los números 28, 21 y 14 no pueden dividirse simultáneamente por 3, este número primo se desecha.
De forma similar se desecha el 5.
El siguiente número primo en la lista es 7.
En este caso se puede hacer la división simultáneamente obteniéndose los números 4, 3 y 2.
Esta última fila no puede dividirse simultáneamente ni por 2 ni por 3.
Como el siguiente número primo (5) es mayor que 4, el proceso termina.
Por lo tanto, el mcd de los números 56, 42 y 28 es el producto de los números primos de la derecha: 2 • 7 = 14
Lo anterior se expresa como: mcd (56, 42, 28) = 14 (el máximo común divisor de los números 56, 42 y 28 es igual a 14)
Ejemplo: Factorizar 9x + 6y - 12z
Este es un ejemplo sencillo de la factorización por factor común.
Dada una expresión algebraica se encuentra el máximo común divisor (mcd) de los coeficientes de los términos de la expresión algebraica.
Este mcd corresponde al coeficiente del factor común.
Para la parte literal se toman las variables comunes a todos los términos con el menor exponente que aparezca.
Para este ejercicio el mcd de 9, 6 y 12 es 3; además como no hay variables comunes en los tres términos tenemos:
9x + 6y - 12z = 3(3x + 2y - 4z)
es decir 9x + 6y - 12z se ha expresado como el producto de los factores 3 y 3x + 2y - 4z.
Ejemplo: Factorizar 9xy2 + 6y4 - 12 y3z
En este caso además del factor común 3 (mcd de 9, 6, 12) la variable y es común a los tres términos. La menor potencia común es y2 por lo tanto la factorización queda:
9xy2 + 6y4 - 12y3z = 3y2(3x + 2y2 - 4yz)
Los factores en este caso son 3x + 2y2 - 4yz y 3y2. Para verificar, al realizar el producto indicado se obtiene la expresión original:
3y2(3x + 2y2 - 4yz) = (3y2 * 3x) + (3y2 * 2y2) - (3y2 * 4yz)
= 9xy2 + 6y4 - 12y3z
TEMA 13.
*) ECUACION LINEAL Y CUADRATICA
3.1 ECUACIONES RACIONALES DE PRIMER GRADO
Todos los conceptos y procedimientos vistos en la solución de operaciones con fracciones algebraicas se pueden aplicar ahora en la solución de las ecuaciones fraccionarias.
3.1.1 Ecuación fraccionaria
Es aquella ecuación que tiene como fraccionarios los coeficientes de sus términos.

Resolver:


ECUACIONES LINEALES Y CUADRÁTICAS
3.1 ECUACIONES RACIONALES DE PRIMER GRADO
Todos los conceptos y procedimientos vistos en la solución de operaciones con fracciones algebraicas se pueden aplicar ahora en la solución de las ecuaciones fraccionarias.
3.1.1 Ecuación fraccionaria
Es aquella ecuación que tiene como fraccionarios los coeficientes de sus términos.

Resolver:


Ecuaciones Lineales son las que tienen las Variables elevadas a la potencia [ 1 ], ejemplo
Para Resolver un sistema de ecuaciones con 2 variables
x + 2y = 10
x + 3y = 9
Vamos a resoverla por el metodo de igualacion
Despejamos una de las 2 Variables para resolver, vamos a despejar [ x ]
x = 10 - 2y
x = 9 - 3y
Igualamos los resultados
10 - 2y = 9 - 3y
Juntamos de lado izquierdo los terminos que tengas [ y ] y del otro lado de la igualdad los terminos que no tengan [y], y les cambiamos el signo a los terminos que movamos
10 - 2y = 9 - 3y
3y - 2y = 9 - 10
y = - 1
Ahora el valor de [ y = - 1 ] lo sustituimos en la ecuacion original para encontrar el valor de [ x ]
x + 2y = 10
x + 2[-1] = 10
x - 2 = 10
x = 10 + 2
x = 12
Estos son los resultados
======================================…
x = 12
y = - 1
======================================…
***************************
Ecuación Cuadrática,
***************************
Esta debe de tener un termino elevado a la [2da Potencia] y como resultado obtendrás [2 soluciones]
x² + 5x + 6 = 0
Se puede resolver de 2 maneras
Por Factorización y por la Formula General
Por Factorización
x² + 5x + 6 = 0
Debemos de encontrar 2 valores que sumados me den [5] y multiplicados me den [6]
2 + 3 = 5
2 * 3 = 6
(x + 2) (x + 3)
Despeando [ x ], La solución es
x = - 2
x = - 3
Por Formula General
- b ± √[b² - 4ac]
----------------------
………2a
x² + 5x + 6 = 0
Donde:
a = 1
b = 5
c = 6
- 5 + √[5² - 4(1)(6)]
--------------------------
………2(1)
- 5 + √[25 - 24]
--------------------------
………2(1)
- 5 + √[1]
---------------
…2(1)
- 5 + 1
---------
…..2
x = - 2
- 5 - √[5² - 4(1)(6)]
--------------------------
………2(1)
- 5 - √[25 - 24]
----------------------
……2(1)
- 5 - √[1]
---------------
…2(1)
- 5 - 1
---------
…..2
x = - 3
Como vez nos dio el mismo resultado
======================================…
x = - 2
x = - 3
======================================…
Para Resolver un sistema de ecuaciones con 2 variables
x + 2y = 10
x + 3y = 9
Vamos a resoverla por el metodo de igualacion
Despejamos una de las 2 Variables para resolver, vamos a despejar [ x ]
x = 10 - 2y
x = 9 - 3y
Igualamos los resultados
10 - 2y = 9 - 3y
Juntamos de lado izquierdo los terminos que tengas [ y ] y del otro lado de la igualdad los terminos que no tengan [y], y les cambiamos el signo a los terminos que movamos
10 - 2y = 9 - 3y
3y - 2y = 9 - 10
y = - 1
Ahora el valor de [ y = - 1 ] lo sustituimos en la ecuacion original para encontrar el valor de [ x ]
x + 2y = 10
x + 2[-1] = 10
x - 2 = 10
x = 10 + 2
x = 12
Estos son los resultados
======================================…
x = 12
y = - 1
======================================…
***************************
Ecuación Cuadrática,
***************************
Esta debe de tener un termino elevado a la [2da Potencia] y como resultado obtendrás [2 soluciones]
x² + 5x + 6 = 0
Se puede resolver de 2 maneras
Por Factorización y por la Formula General
Por Factorización
x² + 5x + 6 = 0
Debemos de encontrar 2 valores que sumados me den [5] y multiplicados me den [6]
2 + 3 = 5
2 * 3 = 6
(x + 2) (x + 3)
Despeando [ x ], La solución es
x = - 2
x = - 3
Por Formula General
- b ± √[b² - 4ac]
----------------------
………2a
x² + 5x + 6 = 0
Donde:
a = 1
b = 5
c = 6
- 5 + √[5² - 4(1)(6)]
--------------------------
………2(1)
- 5 + √[25 - 24]
--------------------------
………2(1)
- 5 + √[1]
---------------
…2(1)
- 5 + 1
---------
…..2
x = - 2
- 5 - √[5² - 4(1)(6)]
--------------------------
………2(1)
- 5 - √[25 - 24]
----------------------
……2(1)
- 5 - √[1]
---------------
…2(1)
- 5 - 1
---------
…..2
x = - 3
Como vez nos dio el mismo resultado
======================================…
x = - 2
x = - 3
======================================…
TEMA 14.
*) SISTEMAS DE ECUACIONES LINEALES

| EJEMPLO 1: Ecuaciones lineales. | |||||||
|
| EJEMPLO 2: Ecuaciones que no son lineales. | |||||||||
|

| EJEMPLO 3: | |
|
| EJEMPLO 4: | |
|
| EJEMPLO 5: | ||||||
|
| EJEMPLO 6: | |
|
TEMA 15.
*) ANGULOS Y TEORIA DE PITAGORAS
 Quería empezar comentando el motivo por el cual decido realizar una unidad didáctica alrededor del Teorema de Pitágoras. Es indudable el uso que dentro y fuera de las matemáticas se puede, y de hecho, se realiza del teorema de Pitágoras. Dentro de la geometría podemos decir que es el teorema más usado, tanto desde el punto de vista teórico, como del punto de vista práctico como herramienta para calcular ángulos, áreas, distancias, y un largo etcétera. También me gustaría señalar que dentro de la educación secundaria, la geometría tiene un papel importante, y por tanto el teorema de Pitágoras no es sólo conocido sino también usando ampliamente por los alumnos.
Quería empezar comentando el motivo por el cual decido realizar una unidad didáctica alrededor del Teorema de Pitágoras. Es indudable el uso que dentro y fuera de las matemáticas se puede, y de hecho, se realiza del teorema de Pitágoras. Dentro de la geometría podemos decir que es el teorema más usado, tanto desde el punto de vista teórico, como del punto de vista práctico como herramienta para calcular ángulos, áreas, distancias, y un largo etcétera. También me gustaría señalar que dentro de la educación secundaria, la geometría tiene un papel importante, y por tanto el teorema de Pitágoras no es sólo conocido sino también usando ampliamente por los alumnos.
 También quiero comentar que el tema de este trabajo no es en sí muy original, está claro que los trabajos acerca del teorema de Pitágoras son innumerables, y sin llegar más lejos en el texto de este mismo curso, Aventuras en Geometría, ya existe un trabajo dedicado a este mismo tema. No obstante, aunque se den estos puntos negativos para la realización de esta unidad didáctica, diré a su favor que son innumerables los matemáticos que han dedicado su esfuerzo y su tiempo a escribir acerca de este tema, y quizás piense que esta es una buena oportunidad para poner mi granito de arena.
También quiero comentar que el tema de este trabajo no es en sí muy original, está claro que los trabajos acerca del teorema de Pitágoras son innumerables, y sin llegar más lejos en el texto de este mismo curso, Aventuras en Geometría, ya existe un trabajo dedicado a este mismo tema. No obstante, aunque se den estos puntos negativos para la realización de esta unidad didáctica, diré a su favor que son innumerables los matemáticos que han dedicado su esfuerzo y su tiempo a escribir acerca de este tema, y quizás piense que esta es una buena oportunidad para poner mi granito de arena.
DEMOSTRACIONES DEL TEOREMA DE PITÁGORAS
A lo largo de la historia han sido muchas las demostraciones y pruebas que matemáticos y amantes de las matemáticas han dado sobre este teorema. Se reproducen a continuación algunas de las más conocidas.
PLATÓN.
EUCLIDES.
El Teorema de Pitágoras
1. Introducción.
 Quería empezar comentando el motivo por el cual decido realizar una unidad didáctica alrededor del Teorema de Pitágoras. Es indudable el uso que dentro y fuera de las matemáticas se puede, y de hecho, se realiza del teorema de Pitágoras. Dentro de la geometría podemos decir que es el teorema más usado, tanto desde el punto de vista teórico, como del punto de vista práctico como herramienta para calcular ángulos, áreas, distancias, y un largo etcétera. También me gustaría señalar que dentro de la educación secundaria, la geometría tiene un papel importante, y por tanto el teorema de Pitágoras no es sólo conocido sino también usando ampliamente por los alumnos.
Quería empezar comentando el motivo por el cual decido realizar una unidad didáctica alrededor del Teorema de Pitágoras. Es indudable el uso que dentro y fuera de las matemáticas se puede, y de hecho, se realiza del teorema de Pitágoras. Dentro de la geometría podemos decir que es el teorema más usado, tanto desde el punto de vista teórico, como del punto de vista práctico como herramienta para calcular ángulos, áreas, distancias, y un largo etcétera. También me gustaría señalar que dentro de la educación secundaria, la geometría tiene un papel importante, y por tanto el teorema de Pitágoras no es sólo conocido sino también usando ampliamente por los alumnos. Para introducir esta unidad didáctica, comentaré mi deseo de abordarla haciendo uso de un formato formal en el cual entra el comentario de los objetivos, contenido, metodología, materiales y por último evaluación. Dentro del contenido expondré un comentario y biografía de Pitágoras y el pitagorismo, además de un pequeño repaso al cálculo de áreas, el enunciado del teorema de Pitágoras, también incluiré más de una demostración del mismo, algunas aplicaciones dentro y fuera de las matemáticas, etc. Los demás puntos de esta unidad didáctica los orientaré en vista a alumnos de educación secundaria.
 También quiero comentar que el tema de este trabajo no es en sí muy original, está claro que los trabajos acerca del teorema de Pitágoras son innumerables, y sin llegar más lejos en el texto de este mismo curso, Aventuras en Geometría, ya existe un trabajo dedicado a este mismo tema. No obstante, aunque se den estos puntos negativos para la realización de esta unidad didáctica, diré a su favor que son innumerables los matemáticos que han dedicado su esfuerzo y su tiempo a escribir acerca de este tema, y quizás piense que esta es una buena oportunidad para poner mi granito de arena.
También quiero comentar que el tema de este trabajo no es en sí muy original, está claro que los trabajos acerca del teorema de Pitágoras son innumerables, y sin llegar más lejos en el texto de este mismo curso, Aventuras en Geometría, ya existe un trabajo dedicado a este mismo tema. No obstante, aunque se den estos puntos negativos para la realización de esta unidad didáctica, diré a su favor que son innumerables los matemáticos que han dedicado su esfuerzo y su tiempo a escribir acerca de este tema, y quizás piense que esta es una buena oportunidad para poner mi granito de arena.DEMOSTRACIONES DEL TEOREMA DE PITÁGORAS
A lo largo de la historia han sido muchas las demostraciones y pruebas que matemáticos y amantes de las matemáticas han dado sobre este teorema. Se reproducen a continuación algunas de las más conocidas.
DEMOSTRACIONES GEOMÉTRICAS
PITÁGORAS.
Una de las demostraciones geométricas mas conocidas, es la que se muestra a continuación, que suele atribuirse al propio Pitágoras. A partir de la igualdad de los triángulos rectángulos es evidente la igualdad a2 + b2 = c2 |
PLATÓN.
La relación que expresa el teorema de Pitágoras es especialmente intuitiva si se aplica a un triángulo rectángulo e isósceles. Este problema lo trata Platón en sus famosos diálogos. |
EUCLIDES.
La relación entre los catetos y la hipotenusa de un triángulo rectángulo, aparece ya en los Elementos de Euclides. Elementos de Euclides. Proposición I.47. En los triángulos rectángulos el cuadrado del lado que subtiende el ángulo recto es igual a los cuadrados de los lados que comprenden el ángulo recto. Para demostrarlo, Euclides construye la figura que se representa a la derecha. La prueba que da Euclides consiste en demostrar la igualdad de las áreas representadas en el mismo color. |
TEMA 16.
*) DISEÑO GRAFICO Y MATEMATICAS








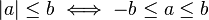
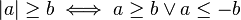

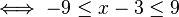
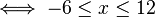

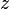 es la distancia
es la distancia  desde
desde 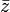 tienen el mismo valor absoluto.
tienen el mismo valor absoluto.